Welcome to DiBS’s documentation!
This is the Python JAX implementation for DiBS: Differentiable Bayesian Structure Learning (Lorch et al., 2021). This documentation specifies the API and interaction of the components of the inference pipeline. The entire code is written in JAX to leverage just-in-time compilation, automatic differentation, vectorized operations, and hardware acceleration.
DiBS translates learning \(p(G | D)\) and \(p(G, \Theta | D)\) over causal Bayesian networks \((G, \Theta)\) into inference over the continuous latent posterior densities \(p(Z | D)\) and \(p(Z, \Theta| D)\), respectively. This extended generative assumptions is illustrated by the following graphical model:
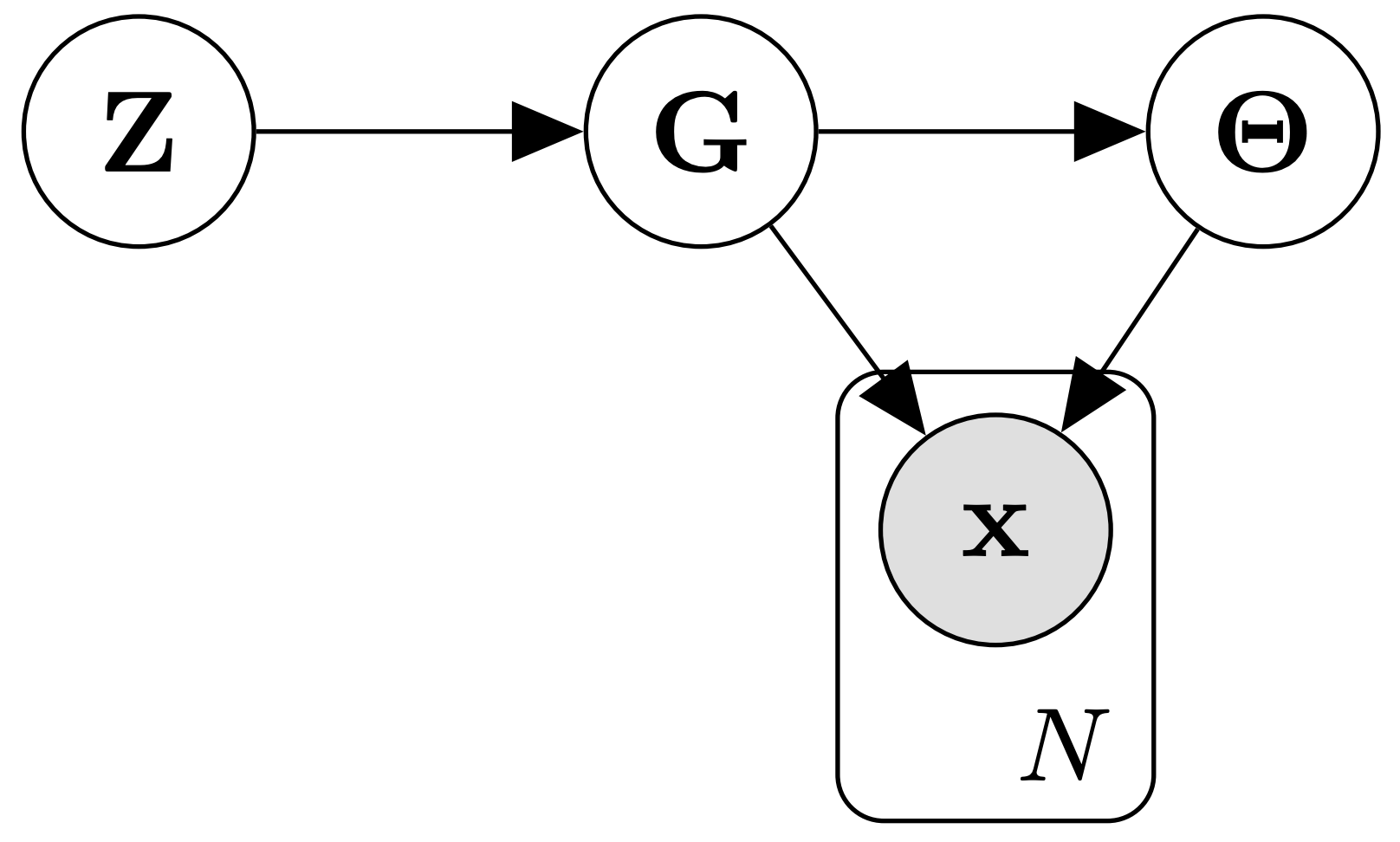
Since we can efficiently estimate the scores \(\nabla_Z \log p(Z | D)\) and \(\nabla_Z \log p(Z, \Theta | D)\), general-purpose approximate inference methods apply off-the-shelf. Further information and experimental results can be found in the paper.
Inference
In this repository, DiBS inference is implemented with the particle variational inference method Stein Variational Gradient Descent (SVGD) (Liu and Wang, 2016). To generate samples from \(p(Z | D)\), we randomly initialize a set of particles \(\{ Z_m \}\) and specify some kernel \(k\) and step size \(\eta\). Then, we repeatedly apply the following update in parallel for \(m=1\) to \(M\) until convergence:
\(\displaystyle Z_m \leftarrow Z_m +\eta \phi(Z_m) ~\text{where}~ \phi(\cdot) := \frac{1}{M} \sum_{k=1}^M k(Z_k, \cdot) \nabla_{Z_k} \log p(Z_k | D ) + \nabla_{Z_k} k(Z_k, \cdot)\)
where at each step \(\nabla_{Z_k} \log p(Z_k | D )\) is estimated for each \(Z_k\) using the REINFORCE trick or Gumbel-softmax reparameterization. The analogous procedure applies when sampling from \(p(Z, \Theta | D)\), where SVGD jointly transports particles \(Z\) and \(\Theta\).